Kurs
3.1
To Infinity and beyond!
Unendlichkeit, Vollständigkeit und Kompaktheit in Funktionalanalysis
Zur Akademie Grovesmühle 2025-3
10.07.
-
26.07.2025
Beinahe unbegreiflich ist heute, wie sich frühere Mathematiker gegen das aktual Unendliche, gegen die Verwendung von Bezeichnungen für unendliche Mengen wie ℕ (natürliche Zahlen) oder ℚ (rationale Zahlen) sträubten. Wegen ihrer Paradoxien blieb die Unendlichkeit (definiert als alles nicht Endliche) lange verworren. Insbesondere dank Cantor und Dedekind konnte sich die Mathematik Ende des 19. Jhs. mit der Unendlichkeit aussöhnen. Einige dieser sonderbaren, ’paradiesischen’ (Hilbert) Verflechtungen, der kontraintutiven Kontraste von endlich und unendlich, werden in diesem Kurs untersucht.
Von Mächtigkeiten und Antinomien, von der Vollständigkeit der reellen Zahlen bis zu Intervallschachtelungen und Existenzsätzen, von der Konvergenz bis zur Stetigkeit, so nimmt der Kurs zuerst Anlauf in der eindimensionalen Analysis der reellen Zahlen.
Mit diesen Werkzeugen ausgestattet widmet sich der Kurs unendlichdimensionalen Räumen, Folgenräumen und Funktionenräumen, metrischen Räumen und topologischen Räumen, insbesondere auch Charakterisierungen der Kompaktheit. Ein einfaches Beispiel eines unendlichdimensionalen Objektes ist der Folgenraum der 0-1-Folgen (Abbildung 1). Mit einem Abstand versehen, ähnlich zum Abstand in den reellen Zahlen, wird daraus ein interessanter metrischer Raum, der zudem direkt zu Kompaktheit oder Fraktalen (Abbildung 2) führt. Das Ziel wird sein, einige deutliche Unterschiede von endlich und unendlich zu untersuchen, von endlichdimensionalen Räumen wie den reellen Zahlen und unendlichdimensionalen Räumen wie dem Raum aller beschränkten reellen Folgen.
Der Kurs unternimmt auch nichtmathematische Exkurse zu Paradoxien, Logik oder Philosophie, die sich aus der Beschäftigung mit Unendlichkeit, Dimension und Topologie ergeben. In der Kursarbeit und etlichen Projekten werden auch eigene mathematische Aussagen aufgestellt und bewiesen, sowie viele Beweismethoden erlernt. Der Kurs setzt sich (ungefähr) aus 3/4 Mathematik sowie 1/4 Exkursen zusammen und hat keine weiteren Voraussetzungen (außer ein gigantomanisches Interesse an obigen Themen).
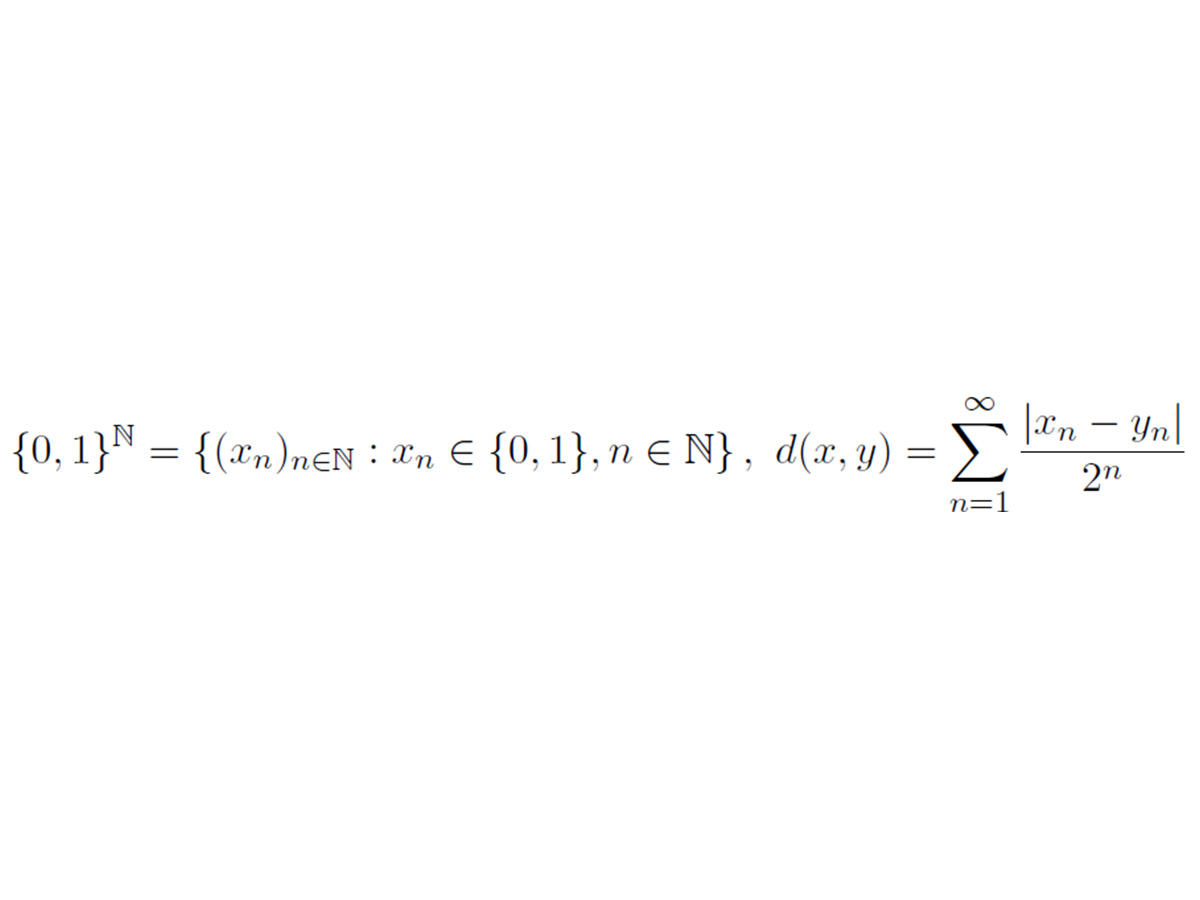
Abbildung 1: Der 0-1-Folgenraum mit Abstandsfunktion

Abbildung 2: Ein Fraktal (eine mächtige kompakte Menge) erzeugt durch vier einfache lineare Funktionen (eigene Darstellung)
Die
Kursleitung


